반응형
통계적 추론의 분류
- 모집단에 대한 가정 여부에 따른 통계적 추론의 분류
모수적 추론
- Parametric Infererence, 모집단에 특정 분포를 가정하고 모수에 대해 추론함
비모수적 추론
- Non-parametric Infererence, 모집단에 대해 특정 분포 가정을 하지 않음
추론 목적에 따른 통계적 추론의 분류
추정
- Estimation, 통계량을 사용하여 모집단의 모수를 구체적으로 추측하는 과정
- 점 추정 : Point estimation, 하나의 값으로 모수의 값이 얼마인지 추측함
- 구간 측정 : Interval estimation, 모수를 포함할 것으로 기대되는 구간을 확률적으로 구함
- 가설검정 Testing hypotheses
- 모수에 대한 가설을 세우고 그 가설의 옳고 그름을 확률적으로 판정하는 방법론
- 모수처리방식에 따른 통계적 추론의 분류
- Frequentist
- Bayesian
표준편차(Standard Deviation)
표준편차
- 자료가 평균을 중심으로 얼마나 퍼져있는지를 나타내는 대표적 수치
- 편차(관측값-평균)

표준오차(Standard Error)
표준편차
- 한 표본에서 전체 개체가 가지는 값들의 차이가 얼마나 큰지 나타냄
표준오차 SE
- 표본집단의 평균값이 실제 모집단의 평균값과 얼마나 차이가 있는지 나타냄
- 오차(추정값 - 점값)
- 모집단에서 샘플을 무한 번 뽑아서 각 샘플마다 평균을 구했을 때, 그 평균들의 표준 편차를 표준오차라 할 수 있음
- 표본평균이 모평균과 얼마나 떨어져 있는가를 나타냄, n이 클수록 작은 값
- 모평균에 대해 추론할 때 표본평균의 표준오차를 사용함
- SE(Standard error=

- 표본을 샘플링 할 때, 모집단을 대표할 수 있는 전형적인 구성요소를 선택하지 못함으로써 발생하는 오차
- 표본의 크기를 증가시키고, 표본 선택 방법을 엄격히 하여 줄일 수 있음
오차한계
- 추정(estimation)을 할때 모평균 추정구간의 중심으로부터 최대한 허용할 최대허용오차
- 추정 문제에서 표준오차를 구하라는 것은 '오차한계'를 구하라는 것과 같음
- 오차한계는 임계값(critical value)와 표준오차(SE)를 곱한 값
- 임계값 : 표준정규분포에서는 z값, t분포에서 t값, 카이제곱분포에서는 카이제곱값
- 표본오차 =오차한계 = 임계값 * a/루트(n)
추정량(estimator)
- 추정이란 표본의 통계량(평균,분산,표준편차)를 가지고 모집단의 모수를 추측하여 결정하는 것

좋은 추정향 판단 기준
일치성(consistency)
- 표본의 크기가 커짐에 따라 표본오차가 작아져야 한다
비편향성,불편성(unbiasedness)
- 편향(bias) = 추정량의 기댓값 - 실제값(=모수의 값) = E(∞)-∞
- 추정량의 기댓값이 모수의 값과 같아야한다(편향==0)
효율성(efficiency)
- 추정량의 분산이 될 수 있는 대로 작아야한다.(최소분산 추정량)
- MSE(Mean Square Error)가 작아야한다
점추정 17,21,22출제
점추정
- Point estimation, 통계량 하나를 구하고 그것을 가지고 모수를 추정하는 방법
- 모수가 특정한 값일 것이라고 추정하는 것
점추정량 구하는 법
- 적률법 - 표본의 기댓값을 통해 모수를 추정하는 방법
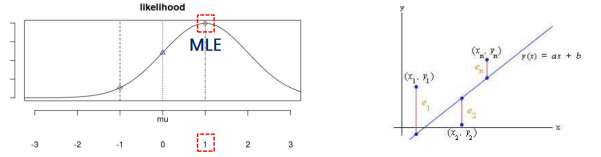
- 최대가능도추정법(최대우도법) - 함수를 미분해서 기울기가 0인 위치에 존재하는 MLE(maximum likelihood estimator)를 찾는 방법
- 최소제곱법 - 함수값과 측정값의 차이인 오차를 제곱한 합이 최소가 되는 함수를 구하는 방법
구간추정 17,21,22출제
구간추정
- Interval esimation, 점추정의 정확성의 정확성을 보완하는 방법
- 통계량을 제시하는 것은 같지만 신뢰구간을 만들어서 추정하는 것
신뢰구간
- 모수가 포함되더리라고 기대되는 '범위'
신뢰수준
- 모수값이 정해져 있을 때 다수 신뢰구간 중 모수값을 포함하는 신뢰구간이 존재할 확률
- 신뢰수준 95% 의미: n번 반복 추출하여 산정하는 신뢰구간들 중에서 평균적으로 95%는 모수 값들을 포함하고 있을 것이라는 의미
신뢰구간

가설검정
가설검정
- Statistical hypothesis testing, 모집단에 대한 어떤 가설을 설정한 뒤에 표본관찰을 통해 그 가설의 채택 여부를 결정하는 통계적 추론 방법
귀무가설(H0)
- null hypothesis, 가설검정의 대상이 되는 가설, 연구자가 부정하고자하는 가설
- 설정한 가설이 진실할 확률이 극히 적어 처음부터 버릴 것(기각)이 예상되는 가설
대립가설(H1)
- anti hypothesis,귀무가설이 가각될 때 받아들여지는 가설
- 연구자가 연구를 통해 입증 또는 증명되기를 기대하는 예상이나 주장
기각역(critical region)
- 검정통계량(t-value)의 분포에서 유의수준의 크기에 해당하는 영역
- 계산한 검정통계량의 유의성(귀무가설의 기각)을 판정하는 기준
제1종 오류
- a(알파) error, 귀무가설이 참인데 기각하게하게 되는 오류
제 2종 오류
- b(베타)error, 귀무가설이 거짓인데 채택하는 오류
유의수준(∑)
- Significance level,제 1종오류의 최대 허용한계
- 유의수준 0.05(5%) : 100번 실험해서 1종 오류 범하는 최대 허용한계가 5번
유의확률 p-value
- Probability Value, 0 ≤ p-value ≤ 1, 1종 오류를 범할 확률, 귀무가설을 지지하는 정도
- 귀무가설이 사실일 때, 기각하는 1종 오류 시 우리가 내린 판정이 잘못 되었을 확률
- 검정 통계량에 관한 확률로, 극단적인 표본 값이 나올 확률
- p-value가 작을 수록 그정도가 약하다고 보며, p-value < a(알파) 귀무가설을 기각,대립가설을 채택함
- p-value가 0.05(5%) : 귀미가설을 기각했을 때 기각 결정이 잘못될 확률이 5%임
-귀무가설을 이용한 가설 검증 프로세스

모수적 , 비모수적 추론 18,21,23회 출제
모수적 추론
- 모집단에 특정 분포를 가정하고 분포의 특성을 결정하는 모수에 대해 추론하는 방법
- 모수로는 평균,분산 등을 사용
- 자료가 정규분포, 등간척도, 비율척도인 경우 (온도, 물가지수, 몸무게, 자녀수,...........)
비모수적 추론
- 모집단에 대해 특정 분포 가정을 하지 않음
- 모수 자체보다 분포형태에 관한 검정을 실시함
- 표본 수가 적고, 명목척도, 서열척도 인 경우 (성별, 혈액형, 만족도, 메달,....................)

모수적 추론(inference)
모수적 검정
- 검정하고자 하는 모집단의 분포에 대해 가정을 하고 그 가정하에서 검정 통계량과 검정 통계량의 분포를 유도해 검정을 실시함
- 가정된 분포의 모수에 대해 가설검정
- 관측된 자료를 이용해 구한 표본평균,표본분산 등을 이용해 검정 실시
모수적 통계의 전체조건
- 표본의 모집단이 정규분포를 이루어야하며, 집단 내의 분산은 같아야함
- 변인(=변수)은 등간척도나 비율척도로 측정되어야함(아니면 비모수 통계사용)
모수 검정방법
- T test, Paired T test, ANOVA test, z분포,t분포,F분포(ANOVA에서 사용)
모수 검정방법 사용 예
- 모평균과 표본평균과의 차이 : z분포, t분포
- 표본평균 간의 차이 : z분포, t분포
- 모분산과 표본분산과의 차이 : F분포
모수적 추론 : T-test
T-test
- 평균값이 올바른지, 두 집단의 평균 차이가 있는지를 검증하는 방법으로 t값을 사용함
- t값이 커질수록 p-value는 작아지며, 집단간 유의사한 차이를 보일 가능성이 높아짐
| t-검정방법 | 예시 |
| One Sample t-test | 단일 표본의 평균 검정을 위한 방법 S사 USB의 평균 수명은 20000시간이다 |
| Paired t-test 대응표본 t-검정 | 동일 개체에 어떤 처리를 하기전, 후의 자료를 얻을 때 차이 값에 대한 평균 검정을 위한 방법 예)매일 1시간 한달 걸으면 2Kg이 빠진다.(걷기 수행 전/수행 후) 가능한 동일한 특성을 갖는 두 개체에 서로 다른 처리를 하여 그 처리의 효과를 비교하는 방법(matching) 예)X질병 환자들을 두 집단으로 나누어, A,B 약을 투약해 약의 효과를 비교 |
| Two sample t-test 독립표본 t-검정 | 서로 다른 두 그룹의 평균을 비교하여 두 표본의 차이가 있는지 검정하는 방법 귀무가설 - 두 집단의 평균 차이 값이 0이다 2학년과 3학년의 결석률은 같다 |
자유도(Degree of freedom)
자유도
- 통계적 추정에서 표본자료 중 모집단에 대한 정보를 주는 독립적인 자료의 수
- n개의 데이터를 이용해 어떤 통계량 A를 계산하고자 할 때 필요한 다른 통계량 B가 있다면 B는 A를 계산하기 전에 고정된 값을 가져야 하고 이것이 자유도에서 제외된다
- 다른 통계량을 한개 사용한 크기가 n인 표본의 자유도 : n-1,관측값(X1,X2,X3,..................................Xn)
- 표본평균의 자유도 : n
- 표본분산에서 자유도 : n-1
- ex)1,3,5,7,9 데이터는 합계가 25이고, 평균이 5이다
- 이때 숫자 하나를 모르더라도 평균을 알면 그 숫자를 찾아낼 수 있다
- 즉 표본 평균 값을 알고 있으면 전체 자료 중 자유롭게 값을 취할 수 있는 관찰치의 개수는 4개이다. df : n-1
One sample T-test
- 임금의 평균이 100이다

Paired T-test(대응표본 t-검정)
- 수면 유도제 데이터를 통한 '두 집단의 평균이 같다'는 가설에 대한 Paired t-test

Two sample T-est(독립표본 t-test)
- 수면유도제 데이터를 통한 '집단 간 평균이 같다'는 가설에 대한 t-test

비모수적 추론(inference) 17회 출제
비모수적 검정
- 모집단의 분포에 대해 제약을 가하지 않고 검정을 실시하는 검정 방법
- 모수 자체보다 분포 형태에 관한 검정을 표시함
- 가설을 "분포의 형태가 동일하다","분포의 형태가 동일하지 않다"와 같이 분포 형태에 대해 설정함
- 관측 값들의 순위나 두 관측 값 사이의 부호 등을 이용해 검정
- 모집단의 특성을 몇개의 모수로 결정하기 어려우며 수 많은 모수가 필요할 수 있음
- 모수적 방법보다 훨씬 단순함, 민감성을 잃을 수 있음
비모수적 검정의 종류
- 명목척도 기준 : 카이스퀘어 검정(Chi-sqquare test), McNemar test, Cocharan test
- 서열척도 기준 : Kolmogorov-Smimov test,Sign Test, Willcoxon signed rank test, Friedman test, Mann-Whitney U Test, Kruskal-Walls H test
모수 / 비모수적 추론방법
| 비교대상 집단 수 | 관계 | 비모수 - 명목척도 | 비모수 - 서열척도 | 모수 |
| 1 | 카이스퀘어 검정 | Kolmogorov Smirnov test | One sample test | |
| 2 | 독립 | Crosstab | Mann-Whitney U test | Two sample test |
| 대응자료 | McNemar test | Wilcoxon signed-rank test Sign test |
Paired T test | |
| K(다변량) | 독립 | Kruskal-Wallis H test | ANOVA test(분산분석) | |
| 대응자료 | Cochran test | Friedman test |
R의 기초 통계 계산

반응형
'빅데이터분석준전문가자격증' 카테고리의 다른 글
| ADsP. PART.3 - 데이터 분석 - 통계분석 - 상관(Correlation)분석 (0) | 2022.06.28 |
|---|---|
| ADsP. PART.3 - 데이터 분석 - 통계분석 - 군집(clustering)분석 (0) | 2022.06.28 |
| ADsP. PART.3 - 데이터 분석 - 통계분석 - 통계학개론 - 2 (0) | 2022.06.27 |
| ADsP. PART.3 - 데이터 분석 - 통계분석 - 통계학개론 - 1 (0) | 2022.06.27 |
| ADsP. PART.3 - 데이터 분석 - 통계분석 - 기초통계분석 (0) | 2022.06.26 |