회귀분석(Regression Analysis)
용어정리
독립변수
- 다른 변수에 영향을 받지 않고 독립적으로 변화하는 수, 변수라고도 함
- 입력 값이;나 원인을 나타내는 변수, y=f(x)에서 x에 해당하는 것
종속변수
- 독립변수의 영향을 받아 값이 변화하는 수, 분석에 대상이 되는 변수
- 결과물이나 효과를 나타내는 변수, y=f(x)에서 y에 해당하는 것
전차(오차항)
- 계산에 의해 얻어진 이론 값과 실제 관측이나 측정에 의해 얻어진 값의 차이
- 오차(Error) - 모집단 , 잔차(Residual) - 표본집단
-회귀분석
- 변수와 변수 사이의 관계를 알아보기 워한 통계적 분석 방법
- 독립변수의 값에 의해 종속변수의 값을 예측하기 위함
- 일반 선형회귀는 종속변수가 연속형 변수일 때 가능함
- 이산형 - 명목척도, 서열척도, 연속형 - 구간척도,비율척도
회귀모형
- 선형회귀모형
-x와 y가 1차식으로 나타날 때의 모형
단순회귀모형(독립변수 1개일 때)

단순회귀분석 - 최소자승법
- 최소자승법(Least Square Method)
- Y = F(x)의 측정값 yi와 함수값 f(x)의 차이를 제곱한 것의 합이 최소가 되도록 Y=F(X)를 구하는 것
- Y-aX + b일 때 잔차를 제곱한 것의 합이 최소가 되도록 하는 상수 a,b를 찾는 것
- 즉,(측정값 - 함수값)^2의 합이 쵀ㅣ소가 되는 직선의 그래프를 찾는 것
- 큰폭의 잔차에 대해 보다 더 큰 가중치를 부여하여, 독립변수 값이 동일한 평균치를 갖는 경우 가능한 한 변동 폭이 적은 표본회귀선을 도출하기 위한 것
단일 회귀모형의 예

- runif(개수,시작,끝) : 시작 ~ 끝 범위에서 개수 만큼의 균일분포를 따르는 난수 발생
- rnorm(개수,평균,표준편차) : 특정평균 및 표준편차를 갖으며 정규분포를 따르는 난수 발생 평균,표준편차 생략 시 평균 0, 표준편차 1
- Im(y~x,data=df) : df에서 y를 종속변수, x를 독립변수호 회귀모형 생성
다중 회귀 모형의 예

*******************************회귀방정식 매우 중요 자주 출제되는 문제*********************************
본 이미지의 회귀방정식의 이미지대로
Coefficients:(Intercept) u v w 3.4374 0.4676 0.9556 -1.9923 일 경우 다음가 같은 회귀방정식이 구해진다y = 3.4374 + 0.4676u+0.9556v-1.9923w라는 회귀방정식이 구해지며, 본 회귀방정식은 문제의 이미지가 주어지고 값을 구하라는 방식으로 출제가 많이 되니, 주의바람.....(참고 : 매우 쉬움, 답을 알려준거와 진배 없음)
회귀모형의 가정 ****************************************************매우자주출제**************************************************
- 회귀모형의 가정, 모델진단 그래프
- 선형성 : 독립변수의 변화에 따라 종속변수도 변화하는 선형(Inear)모형이다
- 독립성 : 잔차와 독립변수의 값이 관련되어 있지 않다 (Durbin-Watson 통계량확인)
- 정규성 : 잔차항이 정규분포를 이뤄야 한다
- 등분산성 : 잔차항들의 분포는 동일한 분산을 갖느다
- 비상관성 : 잔차들끼리 상관이 없어야 한다.
Nonrmal Q-Q plot
- 정규셩(정상성) , 잔차가 정규분포를 잘 따르고 있는지를 확인하는 그래프
- 잔차들이 그래프 선상에 있어야 이상적임
Scale - Location
- 등분산성,y축이 표준화 잔차를 나타내며, 기울기 0인 직선이 이상적임
Cook`s Distance
- 일반적으로 1 값이 넘어가면 관측치를 영향점(inflience points)로 판별

회귀모형의 가정
Residuals vs Fitted
- y축은 잔차, 선형회귀에서 오차는 평균 0이고, 분산이 일정한 정규분포를 가정하므로 y값은 기울기가 0인 직선이 이상적임

회귀모형 핵석(평가방법)
표본 회귀선의 유의성 검정
- 두 변수 사이에 선형관계가 성립하는 지 결정 하는 것으로 회귀식의 기울기 계수 B(베타)i = 0 일 때 귀무가설,B(베타)i ≠일 때 대립가설로 설정한다
회귀모형 해석
- 모형이 통계적으로 유의미한가?
- f통계량,유의확률(p-value)로 확인
- 회귀계수들이 유의미한가?
- 회귀계수의 t값, 유의확률(p-value)로 확인
- 모형이 얼마나 설명력을 갖는가?
- 결정계수(R^2)로 확인
- 모형이 데이터를 잘 적합하고 있는가?
- 잔차 통계량 확인, 회귀진단 징행(선형성 ~ 정상성)
F통계량.P-value
- F 통계량 = 회귀제곱평귶(MSR)/잔차제곱평균(MSE)
- F 통계량에 대한 p-value <0.05
t값,p-value
- t값 - Estimate(회귀계수)/Std.Error(표준오차)
- t값에 대한 p-value < 0.05
결정계수(R^2)
- 70 ~ 90%
F통계량
- 모델의 통계적 유의성을 검정하기 위한 검정 통계량(분산 분석)
- F통계량 = 회귀제곱평균(MSR) / 잔차제곱평균(MSE)
- F통계량이 클수록 회귀 모형은 통계적으로 유의하다, p-value < 0.05 일 때 유의함
결정계수R^2 = SSR/SST
- 회귀식의 적합도를 재는 척도
- 결정계수(R^2) = 회귀제곱합(SSR) / 총제곱합(SST),1-(SSE/SST)
- 결정계수는 0~1사이의 범위를 갖음
- 전체 분산 중 모델에 의해 설명되는 분산의 양
- 결정계수가 커질수록 회귀방정식의 설명력이 높아짐


다중 공선성
-다중 공선성(Multicollinearity)
- 모형의 일부 설명변수(=예측변수)가 다른 설명변수와 상관되어 있을 때 발생하는 조건
- 중대한 다중 공선성은 회귀계수의 분산을 증가시켜 불안정하고 해석하기 어렵게 만들기 때문에 문제가 됨
- R의 vif함수를 사용해 구할 수 있으며, VIF값이 10이 넘으면 다중공선성이 존재한다고 봄
- 해결방법
- 높은 상관 관계가 있는 설명변수 모형을 제거하는 것으로 해결
- 설명변수를 제거하면 대부분 R-square가 감소함
- 단계적 회귀분석을 이용하여 제거
- 설명변수의 선택원칙
- y에 영향을 미칠 수 있는 모든 설명변수 x들을 y의 값을 예측하는 데 참여시킴
- 설명변수 x들의 수가 많아지면 관리에 많은 노력이 요구되므로 가능한 범위 내에서 적은 수의 설명변수를 포함시켜야함
- 두 원칙이 이율배반적으므로 적절한 설명변수 선택이 필요함
셜명변수 선택 방법 18,19,22,33*2회 출제
모든 가능한 조합
- 모든 가능한 독립변수들의 조합에 대한 회귀모형을 고려해 AIC,BC의 기준으로 가장 적합한 모형 선택
- AIC,BIC : 최소자승법의R^2와 비슷한 역할을 하며, 적합성을 측정해주는 지표로, R^2는 큰 값이 좋지만, AIC,BIC는 작을 값이 좋음
후진제거법
- Backward Elimination, 독립변수 후보 모두를 포함한 모형에서 출발해 제곱합의 기준으로 가장 적은 영향을 주는 변수로부터 하나씩 제거하면서 더이상 유의하지 않은 변수가 없을 때까지 설명변수를 제거하고, 이 때 모형을 선택
전진제거법
- Forward Selection, 절편만 있는 모델에서 출발해 기준 통계치를 가장 많이 개선시키는 변수를 차례로 추가하는 방법
단계별 선택법
- Stepwise method, 모든 변수가 포함된 모델에서 출발해 기준 통계치에 가장 도움이 되지 않는 변수를 삭제하거나, 모델에서 빠져있는 변수 중에서 기준 통계치를 가장 개선 시키는 변수를 추가함
회귀모델에서 변수 선택을 위한 판단 기준
- Cp,AIC,BIC등이 있으며, 갑이 작을 수록 좋음
후진제거법을 이횽한 방법


-전진선택법을 이용한 방법

과적합(Overfitting) 33회 출제
과적합의 문제와 해결방법
- 주어진 샘플들의 설명변수와 종속변수의 관계를 필요이상 너무 자세하고 복잡하게 분석
- 샘플에 심취한 모델로 새로운 데이터가 주어졌을 때 제대로 예측해내기 어려울 수 있음
- 해결방법으로 Feature의 개수를 줄이거나, Regularization을 수행하는 방법이 있음

Regularization
- 정규화(Regularization)개념
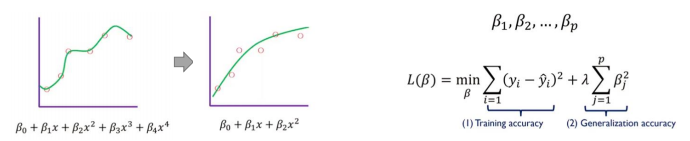
- 베타(B)값에 제약(penalty)을 주어 모델에 변화를 주는 것
- ¤(파이)값은 정규화 모형을 조정하는 hyper parameter
- ¤(파이)값이 클수록 제약이 많아져 적은 변수가 사용되고, 해석이 쉬워지지만 underfitting됨
- ¤(파이)값이 작아질수록 제약이 적어 많은 변수가 사용되고, 해석이 어려워지며, overfitting됨
L1,L2 Norm
- norm : 선형대수학에서 백터의 크기(magnitude) 또는 길이 (length)를 측정하는 방법
L1 norm(=Manhattan norm,맨하튼 거리) : 백터의 모든 성분의 절대 값을 더함
L2 norm(=Euclidean norm,유클리드 거리) : 출발점에서 도착점까지의 거리를 직선거리로 측정함

Regularized Linear Regression 16,23회 출제
라쏘(Lasso)회귀 특징
- 변수 선택이 가능하며, 변수간 상관관계가 높으면 성능이 떨어짐
- L1 Norm을 패널티를 가진 선형 회귀 방법, 회귀계수의 절대값이 클수록 패널티 부여
- MSE가 최소가 되게 하는 w,b를 찾는 동시에 w의 절대값 들의 합이 최소가 되게 해야함
- w의 모든 원소가 0이 되거나 0에 가깝게 되게 해야함 =>불필요한 특성 제거
- 어떤 특성은 모델을 만들 때 사용되지 않게 됨
라쏘(Lasso)회귀 장점
- 제약 조건을 통해 일반화된 모형을 찾는다
- 가중치들의 0이 되게 함으로써 그에 해당하는 특성들을 제외해준다
- 모델에서 가장 중요한 특성이 무엇인지 알게되는 등 모델 해석력이 좋아진다

Ridge 회귀 특성
- L2 norm을 사용해 패널티를 주는 방식
- 변수 선택이 불가능,변수 간 상관관계가 높아도 좋은 성능
- Lasso는 가중치들이 0이 되지만, Ridge의 가중치들은 0에 가까워질 뿐 0이 되지는 않음
- 특성이 많은데 특성의 중요도가 전체적으로 비슷하면 Ridge가 좀 더 괜찮은 모델을 찾아줄 것이다.

엘라스틱넷 특성
- L1,L2 norm refularization
- 변수 선택 가능
- 변수 간 상관관계를 반영한 정규화
데이터 스케일링(Scaling)
- 데이터 단위의 불일치 문제를 해결하는 방법
- 분석에 사용되는 변수들에 사용 단위가 다를 때 데이터를 같은 기중으로 만듦
정규화 normalization
- 값의 범위를 [0,1]로 변환하는 것

- 100점일 경우 50점은? 50-0/(100)=0.5
표준화standardzation
- 특성의 값이 정규분포를 갖도록 변환하는 것, 평균 0 표준편차 1

'빅데이터분석준전문가자격증' 카테고리의 다른 글
| ADsP. PART.3 - 데이터 분석 - 통계분석 - 통계학개론 - 2 (0) | 2022.06.27 |
|---|---|
| ADsP. PART.3 - 데이터 분석 - 통계분석 - 통계학개론 - 1 (0) | 2022.06.27 |
| ADsP. PART.3 - 데이터 분석 - 데이터 마트 - 3 (0) | 2022.06.25 |
| ADsP. PART.3 - 데이터 분석 - 데이터 마트 - 2 (0) | 2022.06.25 |
| ADsP. PART.3 - 데이터 분석 - 데이터 마트 - 1 (0) | 2022.06.25 |