ADsP. PART.3 - 데이터 분석 - 통계분석 - 분류(Ciassification)분석
데이터 분석 순서
분석용 데이터 준비 => 탐색적 분석 데이터 전처리 => 모델링 => 모델 평가 및 검증 => 모델 적응 운영 방안 수립
속성 간 상관관계 파악 데이터 확인 회귀분석 결정계수(R^2)
데이터 특성 파악 데이터 형식 변경 분류분석 F통계량,t값
분포 파악 결측 값 처리 군집분석 ROC Curve
이상 값 처리 연관분석 오분류표
특성 조작(Scaling, Binning, 실루엣,DI
Transform,Dummery)
데이터 차원 축소
Machine Learning Algorithms

분류분석 종류
- 로지스틱 회귀
- 의사결정나무
- 앙상블
- 신경망모형
- kNN,베이즈분류 모형,SVM(서보트백터기계),유전자 알고리즘
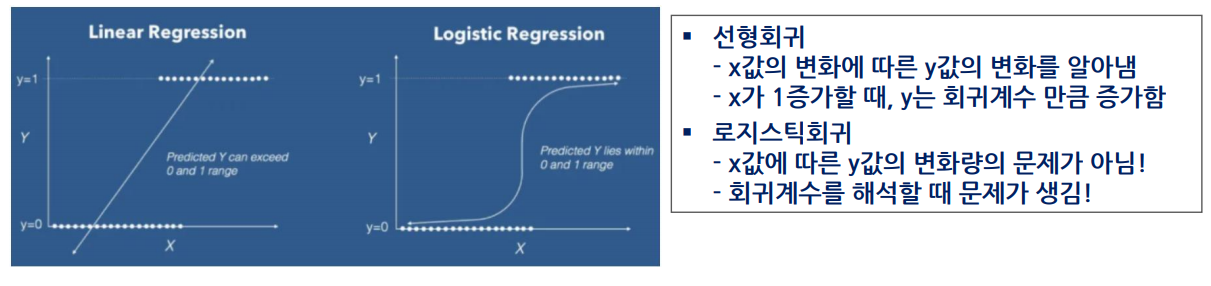
로지스틱 회귀분석 16.18.20,22회 출제
- 독립변수는 연속형, 종속변수가 범주형인 경우 적용되는 회귀분석 모형
- 종속변수가 성공/실패, 사망/생존과 같이 이항변수(0,1)로 되어 있을 때 종속변수와 독립변수 간의 관계식을 이용하여 두 집단 또는 그 이상의 집단을 분류하고자 할 때 사용되는 분석기법
| 일반 선형 회귀분석 | 로지스틱 회귀분석 | |
| 종속변수 | 연속형 변수 | 이산형(범주형)변수 |
| 모형 탐색방법 | 최소자승법(LSM,최소제곱법) | 최대우도법(MLE),가중최소자승법 |
| 모형 검정 | F-Test,T-Test | X^2 Test |
-종속변수를 전체 실수 범위로 확장하여 분석하고, sigmoid 함수를 사용해 연속형 0~1 값으로 변경

로지스틱 회귀분석 (odds) 33회 출제


의사결정나무(Decision Tree)모형
- 의사걀장 규칙을 나무구조로 나타내 전체자료를 몇 개의 소집단으로 분류하거나 예측을 수행하는 분석방법
- 분석과정이 직관적이고 이해하기 쉬움

특징
- 목적은 새로운 데이터를 분류하거나 값을 예측하는 것이다
- 분리변수 P차원 공간에 현재 분할은 이전 분할에 영향을 받는다
- 부모마디보다 자식마디의 순수도가 증가하도록 분류나무를 형성해나간다(불순도 갑소)
종류
- 목표변수(=종속변수)이산형인 경우 분류나무(classification tree)
- 목표변수가 연속형인 경우의 회귀나무
장점
- 구조가 단순하여 해석이 용이함
- 비모수적 모형으로 선형성, 정규성,등분산성 등의 수학적 가정이 불필요함
- 범주형(이산형)과 수치형(연속형)변수를 모두 사용할 수 있음
단점
- 분류 기준값의 경계선 부근의 자료 값에 대해서는 오차가 큼(비연속형)
- 로지스틱 회귀와 같이 각 예측변수의 효과를 파악하기 어려움
- 새로운 자료에 대한 예측이 불안정할 수 있음
의사결정나무의 결정규칙
분리기준
- Split criterion, 새로운 가지를 만드는 기준을 어떻게 정해야 할까?
- 순수도가 높아지는 방향으로 분리
- 불확실성이 낮아지는 방향
정지규칙
- 더 이상 분리가 일어나지 않고 현재의 마디가 최종마디가 되도록 하는 규칙
- '불순도 감소량'이 아주 작을 때 정지함
가지치기 규칙
- 어느 가지를 쳐내야 예측력이 좋은 나무일까?
- 최종 노드가 너무 많으면 Overfitting가능성이 커짐,이를 해결하기 위해 사용
- 가지치기 규칙은 별도 규칙을 제공하거나 경험에 의해 실행할 수 있음
- 가지치기 비용함수(Cost Function)을 최소로 하는 분기를 찾아내도록 학습
- Information Gain이란 어떤 속성을 선택함으로 인해 데이터를 더 잘 구분하게 되는 것을 의미함(불확실성 감소)
불순도 측정 지표
지니지수
- 불순도 측정 지표, 값이 적을수록 순수도가 높음(분류 잘됨)
- 가장 작은 값을 갖는 예측변수가 이때의 최적 분리에 의해 자식마다 형성
- Gini(T) = 1 - ∑(각 범주별 수/전체 수)^2 1-∑^k i=1Pi^2
- 지니지수 : 1-((2/4)+(2/4) = 1-(1/4+1/4)=1/2
엔트로피 지수
- 불순도 측정 지표,가장 작은 값을 갖는 방법 선택
- Entropy(T) : ∑^k i=1 Pilog2pi
카이제곱 통계량의 유의확률(p-value)
- 가장 작은 값을 갖는 방법 선택
의사결정나무를 위한 알고리즘
- 의사결정나무를 위한 알고리즘은 CHAID,CART,ID2,C5.0C4.5가 있으며 하향식 접근 방법을 이용한다
- 알고리즘별 분리, 정지 기준변수 선택법
| 알고리즘 | 이산형 목표변수(분류나무) | 연속형 목표변수(회귀나무) |
| CART (Classification And Regrssion Tree) | 지니지수 | 분산 감소량 |
| C5.0 | 엔트로피지수 | |
| CHAID (Chi-squared Automatic Interaction Detection) |
카이제곱 F통계량의 p-value | ANOVA F통계량 p-value |
앙상블(Ensemble)모형
앙상블 모형
- 여러 개의 분류 모형에 의한 결과를 종합하여 분류의 정확도를 높이는 방법
- 적절한 표본추출법으로 데이터에서 여러 개의 훈련용 데이터 집합을 만들어 각 데이터 집합에 하나의 분류기를 만들어 결합하는 방법
- 약하게 학습 된 여러 모델들을 결합하여 사용
- 성능을 분산시키기 때문에 과적합(Overfitting)감소 효과가 있음
앙상블 모형의 종류
- Voting 부팅
- Bagging 배깅
- Booting 부스팅
- Random Forest 랜덤 포레스트
부팅 Voting
- 서로 다른 여러 개 알고리즘 분류기 사용
- 각 모델의 결과를 취합하여 많은 결과 또는 높은 확률로 나온 것을 최종 결과로 채택하는 것

배깅 Bagging,Bootstrap AGGregatING
- 서로 다른 훈련 데이터 샘플로 훈련, 서로 같은 알고리즘 분류기 결합
- 원 데이터에서 중복을 허용하는 크기가 같은 표본을 여러 번 단순 임의 복원 추출하여 각 표본에 대해 분류기(classifiers)를 생성하는 기법
- 여러 모델이 병렬로 학습, 그 결과를 집계하는 방식
- 같은 데이터가 여러 번 추출될 수도 있고, 어떤 데이터는 추출되지 않을 수 있음
- 대표적 알고리즘 : Meta Algorithm

부스팅 Boosting
- 여러 모델이 순차적으로 학습
- 이전 모델의 결과에 따라 다음 모델 표본 추출에서 분류가 잘못된 데이터에 가중치(weight)를 부여하여 표본을 추출함
- 맞추기 어려운 문제를 맞추는 데 초점이 맞춰져 있고, 이상치(Outlier)에 약함
- 대표적 알고리즘 : AdaBoost, GradientBoost(XGBoost, Light GBM)등

랜덤 포레스트 Random forest
- 배깅(Bagging)에 랜덤 과정을 추가한 방법
- 노드 내 데이터를 자식 노드로 나누는 기준을 정할 때 모든 예측변수에서 최적의 분할을 선택하는 대신, 설명변수의 일부분만을 고려함으로 성능을 높이는 방법 사용
- 여러 개 의사결정 나무를 사용해, 하나의 나무를 사용할 때마다 과적합 문제를 피할 수 있음

k-NN(k-Nearest Neighbors)
- 새로운 데이터에 대해 주어진 이웃의 개수(k)만큼 가까운 맴버들과 비교하여 결과를 판단하는 방법
- k값에 따라 소속되는 그룹이 달라질 수 있음(k값은 hyper parameter)
- 거리를 측정해 이웃들을 뽑기 때문에 스케일링이 중요함
- 반응변수가 범주형이면 분류, 연속형이면 회귀의 목적으로 사용됨
- 모형을 미리 만들지 않고, 새로운 데이터가 들어오면 그때부터 계산을 시작하는 lazy learning(게으른 학습)이 사용되는 지도 학습 알고리즘

SVM(Support Vector Machine)
- Support Vector Machine, 서로 다른 분류에 속한 데이터 간의 간격(margin)이 최대가 되는 선을 찾아 이를 기준으로 데이터를 분류하는 모델
- 아래 그림에서 H3는 분류를 올바르게 하지 못하며, H1,H2는 분류를 올바르게 하는 데 H2가 H1보다 더 큰 간격을 갖고 분류하므로 이것이 분류 기준이 됨