ADsP. PART.3 - 데이터 분석 - 통계분석 - 주성분(Principal Component)분석

주성분 분석(PCA)                       19,20회출제

  주성분분석(PCA,Principal Component Analysis)

• 데이터를 분석할 때 변수의 개수가 많다고 모두 활용하는 것이 꼭 좋은 것이 아님
• 오히려 변수가 '다중공선성'이 있을 경우 분석 결과에 영향을 줄 수 있음
• 공분산행렬 또는 상관계수 행렬을 사용해 모든 변수들을 가장 잘 설명하는 주성분을 찾는 방법
• 상관관계가 있는 변수들을 선형 결합에 의해 상관관계가 없는 새로운 변수(주성분)을 만들고 분산을 극대화하는 변수로 축약함
• 주성분은 변수들의 선형결합으로 이루어져 있음
• 독립변수들과 주성분과의 거리인  '정보손실량'을 최소화하거나 

 - 주성분분석 할 때 고민해야 하는 것

• 공분산행렬과 상관계수행렬 중 어떤 것을 선택할 것인가?
• 주성분의 개수를 몇 게로 할 것인가?
• 주성분에 영향을 미치는 변수로 어떤 변수를 선택할 것인가?

 - 공분산 행렬(default) VS 상관계수 행렬

• 공분산 행렬은 변수의 측정단위를 그대로 반영한 것이고, 상관계수 행렬은 모든 변수의 측정단위를 표준화한 것이다.
• 공분산행렬을 이용한 경우 측정 단위를 그대로 반영하였기 때문에 변수들의 측정단위에 민감하다.
• 주성분분석은 거리를 사용하기 때문에 척도에 영향을 받는다(정규화 전후의 결과가 다르다)
• 설문조사처럼 모든 변수들이 같은 수준으로 점수화 된 경우 공분산행렬을 사용한다
• 변수들의 scale이 서로 많이 다른 경우에는 상관계수행렬(correlation matrix)을 사용한다

주성분분석에서 상관계수 행령 사용

• procomp(data,scale=TRUE)
• princomp(data,cor=TRUE)

-주성분 결정 기준

성분들이 설명하는 분산의 비율

• 누적 분산 비율을 확인하면 주성분들이 설명하는 전체분산 양을 알 수 있음
• 누적 분산 비율이 70~90%사이가 되는 주성분 개수 선택

고윳값(Eigenvalue)

• 분산의 크기를 나타내며, 고윳값이 1보다 큰 주성분만 사용함

Scree Plot

• 고윳값을 가장 큰 값에서 가장 작은 값을 순서로 정렬해 보여줌(1보다 큰 값 사용)

주성분 분석(PCA) 해석 19,20,21,23회 출제

주성분분석 문제

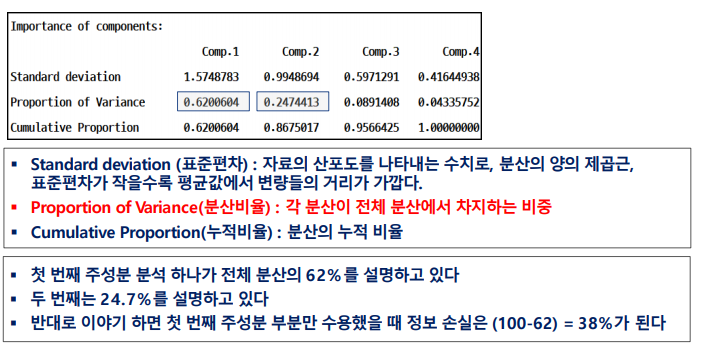
아래는 주성분 분석 결과이다.

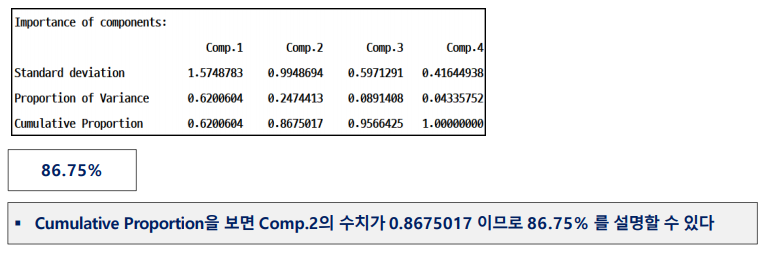
2개의 주성분을 사용한다면 전체 분산의 몇 퍼센트(%)를 설명할 수 있는가?