ADsP. PART.3 - 데이터 분석 - 통계분석 - 통계학개론

빅데이터분석준전문가자격증

ADsP. PART.3 - 데이터 분석 - 통계분석 - 통계학개론 - 1

theblack0 2022. 6. 27. 12:54

통계분석 개요

- Population, Parameter, Sample, Statistic

모집단

잘 정의된 연구목적과 이와 연계된 명확한 연구대상(데이터 전체 집합)
- 예)대통령 후보의 지지율 - 윤권자

모수

모집단의 특성을 나타내는 수치들
모집단의 평균(u(뮤)),분산(a(알파)^2)같은 수치들을 모수(parameter)라고 함

표본

모집단의 개체수가 많아 전부 조사하기 힘들 때 모집단에서 추출(sampleing)한 것
추출(sampling)한 표본으로 모집단의 특성을 추론(infernece)함 (오차발생)
예)각종 여론조사에 참여한 유권자

통계량

표본의 특성을 나타내는 수치들
표본의 평균(xu),분산(s^2)같은 수치를 통계량(statistic)이라고 함

표본 추출 17,33회 추출*********************************************************************************************

- 확률적 표본추출법의 종류

단순 무작위추출 Simple random sampling

모집단의 각 개체가 표본으로 선택될 확률이 동일하게 추출되는 경우
모집단의 개체수 N, 표본 수,n일 때 게뱔 개체가 선택될 확률은 n/N임

계통추출 Systematic sampling

모집단 개체에 1,2,..............N이라는 일련번호를 부여한 후, 첫번째 표본을 임의로 선택하고 일정 간격으로 다음 표본을 선택함
1~100번보 부여 후, 10개 선택한다면,(1,11,21,31,................91)선택

층화추출 Stratified sampling

모집단을 서로 겹치지 않게 몇 개의 집단 또는 층(strata)으로 나누고, 각 집단 내에서 원하는 크기의 표본을 단순 무작위 추출법으로 추출함
층 : 성별,나이대,지역 등 차이가 존재하는 그룹

군집 추출 Cluster sampling

모집단을 차이가 없는 여러 개의 집단(cluster)로 나눔
예)경상대학 내에 경영학과,경제학과
이들 집단 중 몇 개 선택한 후, 선택된 집단 내에서 필요한 만큼의 표본을 임의로 선택함

- 비확률 표본 추출법은 특정 표본이 선정될 확률을 알 수 없어 통계학에서 사용할 수 없음

척도의 종류 19,20*3,22,33*2회 출제*****************************************************************************

명목척도 nominal scale

단순히 측정 대상의 특성을 분류하거나 확인하기 위한 목적
숫자로 바꾸어도 그 값이 크고 작음을 나타내지 않고 범주를 표시함
성별,혈액형,출생지 등

서열(순위,순서)척도 Ordinal scale

대소 또는 높고 낮음 등의 순위만 제공할 뿐 양적인 비교는 할 수 없음
항목들 간에 서열이나 순위가 존재
금,은,동메달,선호도,만족도(Likert 척도)등

등간척도(구간척도) Interval scale

순위를 부여하되 순위 사이의 간격이 동일하여 양적인 비교가 가능함
절대 0점이 존재하지 않음, 온도계 수치, 물가지수
절대 0점이 없음을 의미함
온도의0은 상대 0점으로 없음이 아니라 영상,영하의 중간 지점을 나타냄

비율척도 Ratio scale

절대 0점이 존재하여 측정값 사이의 비율 계산이 가능한 척도
몸무게,나이,형제의 수,직장까지 거리

집중화 경향 측정 21,33회 출제

-집중화 경향(Centeral Tendency)측정에 사용되는 값들

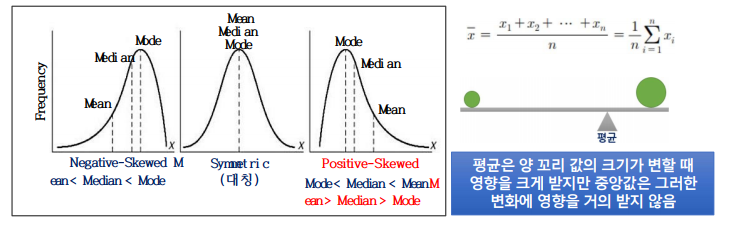
평균(Mean)

값들의 무게 중심이 어디인지를 나타내는 값, 산술 평균

중앙값(Median)

자료를 크기 순서대로 배열했을 때, 중앙에 위치하게 되는 값

최빈값(Mode)

어떤 값이 가장 많이 관찰되는 지 나타낸 값

데이터 퍼짐 정도 측정

- 데이터 집합이 얼마나 퍼저 있는지를 알아보는 데 사용하는 값들

산포도(dispersion)

자료의 변량들이 흩어져 있는 정도를 하나의 수로 나타낸 값
산포도가 크면 변량들이 평균으로부터 멀리 흩어져 있음, 변동성이 커짐
산포도가 작으면 변량들이 평균 주위에 밀집,변동성이 작아짐
범위,사분위수 범위,분산,표준편차,절대편차,변동계수

편차

어떤 자료의 변량에서 평균을 뺀 값을 편차라고 한다(편차 - 변량-평균)
편차의 총합은 항상 0, 편차의 절댓값이 클수록 그 변량은 평균에서 멀리 떨어져 있고, 편차의 절대값이 작을수록 평균에 가까이 있다

분산(s^2) Variance

편차의 제곱의 합을 n-1로 나눈 것
데이터 집합이 얼마나 퍼져있는지 알아볼 수 있는 수치
평균이 같아도 분산은 다를 수 있음

표준편차(s) Standard Deviation

자료의 산포도를 나타내는 수치, 분산의 양의 제곱근
평균으로부터 각 데이터의 관찰 값까지의 평균거리

분산(Variance)의 중요성

평균은 같지만 다른 두확률 분포

분산, 표준편차

분산,표준편차의 이해
- 특정도시의 10가구를 표본으로 추출해 자녀수를 조사한 결과가 0,0,0,1,1,2,2,3,3,3일 때
- 표본 평균 : 1.5 분산 : 1.61, 표준 편차 : 1.27이 나옴
- 특정 도시의 각 가구는 평균 1.5명의 자녀를 가지고, 각 가구는 약 1.27명의 자녀를 더하거나 뺀 범위 안에 있을 것으로 예상

변동 계수(CV,coefficient of variation)

단위가 다른 두 그룹 또는 단위는 같지만 평균차이가 클 때의 산포 비교에 사용함
- A학생이 평균 3시간 공부하고 표준편차는 0.4이었고, B학생은 평균 6시간 공부하고, 표준평차가 0.9이었다면 어떤 학생이 꾸준하게 공부했을까?
- CV=s/x, A=0.4/3 - 0.133, B = 0.9/6 = 0.15이미므로 변동계수가 작은 A가 더 꾸준히 공부함
- 이때, B학생의 표준편차가 0.8이라면 A,B학생의 변동계수가 같아짐, 즉 공부시간이 평균에 대한 표준편차의 비율이 CV임
- 관측되는 자료가 모두 양수일 때 사용

통계 기본용어

표본점

어떤 행위를 했을 때 나올 수 있는 값
주사위 굴리는 행위를 했다면 1,2,3,4,5,6 중 하나

표본공간

모든 표본점의 집합
주사위 굴리는 행위에 대한 표본공간 S={1,2,3,4,5,6}

사건

표본점이 특정한 집합
주사위를 한번 굴렸을 때 홀수가 나오는 사건을 A라고 하면 A={1,3,5}

확률 probability

사건이 일어날 수 있는 가능성을 수로 나타낸 것
어떤 사건을 A라고 했을 때, A가 발생할 확률은 P(A)와 같이 표기함
확률 = 사건/표본공간
확률갑 : 0 ≤ P(A) ≤ 1

사건의 종류 19,33회 출제

독립사건

A의 발생이 B가 발생할 확률을 바꾸지 않는 사건
두 사건A,B가 독립이면, P(B|A) = P(B), P(A|B) = P(A), P(A∩B) = P(A) * P(B)성립
예) 주사위 던져서 나오는 눈의 값과 동정을 던져 나오는 앞/뒤 사건
예)서로 다른 사람이 총을 쏘아 과녁에 명중할 사건

배반사건

교집합이 공집합인 사건, 한쪽이 일어나면 다른 쪽이 일어나지 않을 때의 두 사건
P(A∩B)=0, P(A∪B)= P(A)+P(B)
예)동전 하나를 던져 앞면 나오는 사건, 뒷면 사오는 사건

종속사건

두 사건 A와 B에서 한 사건의 경과가 다른 사건에 영향을 주는 사건
예)음주와 사고 사건, P(A∩B) = P(A|B)P(B)

조건부확률

-조건부확률(Conditional probability)

사건 B가 발생했다는 조건 아래서 사건 A가 발생할 조건부 확률
P(A|B) = P(A∩B)/P(B), 단 P(B) > 0
두 사건 A,B가 독립사건인 경우 : P(B|A) = P(B), P(A|B) = P(A), P(A∩B) = P(A)|P(B)

확률분포 19,23출제

분포

일정한 범위 안에 흩어져 있는 정도

확률분포

random, variable, 확률 현상에 기인해 결과 값이 확률 적으로 정해지는 변수
확률 현산 : 어떤 결과들이 나올지 알지만, 가능한 결과들 중 어떤 결과가 나올지 모르는 현상

이산형 확률분포

Discrete(별개의), 확률변수가 몇개의 한정된 가능한 값을 가지는 분포
각 사건은 서로 독립이어야 함
예)이항분포,베루누이분포,기하분포,포아송분포 등

연속형 확률분포

Contiriuous, 확률번수의 가능한 값이 무한 개이며 사실상 셀수 없을 때
예)정규분포,지수분포,연속균일분포,카이제곱분포,F분포 등

이산형 확률분포

이산형 확률분포 ->베루누이분포 ->이항분포 -> 기하분포 -> 포아송분포

베르누이분포

실험결과 두 가지 중의 하나로 나오는 시행의 결과를 0 또는 1 값으로 대응시키는 확률변수 x에 대해 아래 식을 만족하는 확률변수 x가 따르는 확률분포
P(X=0)=p,(X=1)=q, 0 ≤ p ≤1, q = 1-p
모수가 하나이며 서로 반복되는 사건이 일어나는 실험의 반복적 실행을 확률분포로 나타낸 것

베르누이분포의 예

동전을 던져서 앞면이 나올 확률
- p=1/2, q=1/2
주사위를 던져서 4의 눈이 나올 확률
- p=1/6, q=5/6
주사위를 던져서 4,5,의 눈의 나올 확률
- p = 1/3, q=2/3
이항분포
- 서로 독립된 베르누이 시행을 n회 반복할 때 성공한 횟수를 x라 하면, 성공한 x의 확률분포를 말함
- 확률변수 K가 n,p 두 개의 모수를 갔으며, K-B(n,p)로 표기함
- n=1일 때 이항분포가 베르누이분포임
- 이항분포의 기댓값 E(x)=np
- 이항분포의 분산: V(x)=np(1-p)
이항분포의 예
동전을 50번 던져서 앞면이 나올 경우는?
- n=50, p=1/2
주사위를 10번 던져서 나오는 눈이 5일 경우는?
- n=10,p=1/6
타율 3할인 타자가 100번 타석에 들어서면 안타를 얼마나 칠 것인가?
- n=100, p=0.3
기하분포
베르누이 시행에서 처음 성공까지 시도한 횟수 x의 분포, 지지잡합 (x) = {1,2,3,..............}
베르누이 시행에서 처음 성공할 때까지 실패한 횟수, Y=X-1의 분포, 지지집합(x)={0,1,2,............}
성골확률 p인 베르누이 시행에 대해, x번 시행 후 첫번째 성공을 얻을 확률, X ~ G(p)로 표기
P(X=x) = (1-P)x+1P(x=1,2,3,................)
실패 횟수에 대해서는 P(Y=x)=(1-p)*p (x=0,1,2,...............)

기하분포의 예
- A 야구선수의 홈런 칠 확률이 5%일 때, 이 선수가 x번째 타석에서 홈런 칠 확률분포
포아송분포
- 단위시간이나 단위공간에서 어떤 사건이 몇번 발생할 것인지를 표현하는 분포
- 특정기간 동안 사건(events)발생의 확률을 구할 때 쓰임
- X~Pols(np)
- ∇(파이) : 정해진 시간 안에 어떤 사건이 일어날 횟수에 대한 기댓값, P(X=x) e-A∇^2/x^i
포아송분포의 예
- 어느 AS센터에 1시간당 평균 120건의 전화가 온다. 이때 1분동안 걸려오는 전화 요청이 4건 이하일 확률은?
- 어는 가게에 1시간당 평균 8명의 손님이 온다. 이때, 1시간 동안 손님이 10명 올 확률은?
- 확률은 x=∇에서 최대이며, x가 커질수록 0에 접근함

기댓값

기댓값 : 확률변수 X의 가능한 모든 값들의 가중 평균